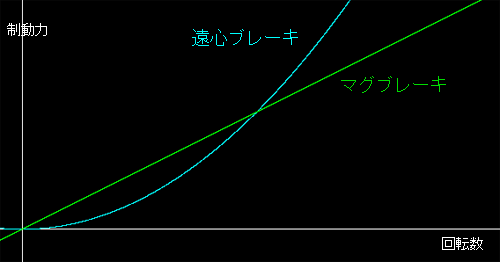
1次関数はy=1/2・x、2次関数曲線はy=1/2・x^2としてみた
なので、実際のリールの制動力と回転数が数値化・座標化されたわけではなく、あくまで概念としての話だ
遠心ブレーキとマグブレーキの決戦というと、「シマノvsダイワ」という図式を連想してしまう。「SVS対マグフォースV」だ。どっちがいいの?そんなのは好みでいいに決まっているぞ。個人の好みだから色々と議論は尽きないだろうし、ネット上でも自らの思いを綴ったサイトもよく見かける。ただ、ライギャーリールの場合はPE10号クラスだとほとんどのリールは遠心ブレーキだったりする。マグブレーキのリールってABUのウルトラマグIII系か6600FLみたいなオールド物?やABU6000番の一部のMAGリールしか存在しなくなる。マグブレーキ代表のダイワですら、ミリオネアの300番は遠心ブレーキだ。なので、別に比べる必要も無いっちゃぁ無いのだが、それを言い出すと何も実験できなくなるからね。
ちなみに管理人の好みは、「う〜ん、どっちでもいいよ、左ハンドルだったら!」と言い切ってしまう。なので、中立な視点で検討することができるだろう。ただ、遠投する場合で弾道を高くして投げた場合には遠心ブレーキの方が制御しやすいとは感じている。だから、今のところライギャー限定という縛りがあるのなら、恐らく「遠心ブレーキの勝ち!」という判定になる様な気がするのだが・・・
実際の比較検討を実施する前に、理論武装をしておく。遠心ブレーキやマグブレーキがどういった理屈で制動力を発生させているかについてだ。遠心ブレーキは簡単だと思うが、マグブレーキは恐らく意味不明だろう。実のところ管理人もマグブレーキのシステムを理解するために、足らないアタマを色々をフル回転させ、なおかつ「フレミングの右手・左手」などという、学生の頃以来聞いたこともないコトバと格闘していたことも付け加えておく。
長ったらしい理論武装がイヤな人のための初級編、結論から先に述べると、
これくらいのお話なら、もしかすると耳にしたことや、目にしたことががあるかも知れない。

1次関数はy=1/2・x、2次関数曲線はy=1/2・x^2としてみた
なので、実際のリールの制動力と回転数が数値化・座標化されたわけではなく、あくまで概念としての話だ
遠心ブレーキの場合で「キャスティング後半のヌケの良さ」というのを耳にしたことがある?あるいは、ダイワのマグフォースVがインダクトローターを遠心力で軸方向に動かして、低回転域で制動力が過大になり過ぎない様にしているのはご存じだと思う。で、上のグラフは制動力を縦軸、スプール回転数を横軸にして、1次関数と2次関数曲線をプロットさせた簡単なものだが、これだけでも2次関数の遠心ブレーキが低回転域での制動力が少ないことがわかると思う。逆に言えば遠心ブレーキは高回転域ではブレーキが効きすぎることになる。調整するのもめんどくさいし。このあたりが遠心ブレーキというシステムの限界かな?
上のグラフでマグブレーキの低速域での制動力を遠心ブレーキのレベルまで少なくする。すると、緑のグラフの傾斜は緩くなり、当然のことながら高回転域で必要な制動力が確保できない。また、高回転域の制動力を確保しようとする。今度は緑のグラフの傾斜はきつくなり、低回転域どころか中速でも制動力が過大になりすぎて全く飛ばないリールになってしまう。マグブレーキで非線形のグラフを描きたければ、現行ダイワのマグフォースVやマグフォースZの様なシステムか、遠心ブレーキ+マグブレーキのツインブレーキみたいに、いずれにしても遠心力を介在させることになる。
それでは中級編、それぞれのブレーキの制動原理について見ていこう
まずは遠心ブレーキだ

これは珍しく右ハンドル、初代?ミリオネアの6Hだ
旧ABUそっくりだが、6000Cスプールは使えんかったりする・・・
こんなのは簡単だとは思うが、一応コメントを残しておこう。
水色の丸いワクがブレーキのリムと考えてほしい。スプールが回転するとブレーキブロックが遠心力をうけて外側に移動する。リムに接触したブレーキブロックと、リムとの間で摩擦が発生し、その摩擦力が遠心ブレーキというシステムの制動力だ。
次はマグブレーキ、電磁誘導の理論だからちょっと難しいぞ

今度はCV-Z253Lなので、ミリ6Hとは逆回転だ
それにしても、ダイワの初代マグサーボの透視画像があれば簡単だったのだが・・・
向かい合った磁石の間の空間には磁界が発生している。その磁界中を電気の導体であるインダクトローターが回転すると磁界に変化が生じる。すると導体には誘導起電力が発生し、誘導起電力により発生した電流は磁界の変化を妨げる方向に流れる。発電機はこの原理で発電している。で、誘導電流の方向は「フレミングの右手の法則」によって求められる。

懐かしのフレミングの右手だ
左も右も、中指から「電・磁・力」って覚えていたような気がする・・・
この右手を上のCV-Zの画像に当てはめてみると(みんなもやってみてね)、親指を左に向け、人差し指を下に向ければ中指は手前を向いているはず。なので、誘導電流は奥から手前に流れることになる。ただ、妨げる方向に電流が流れただけではまだ不完全だ。なのでもう少し考えなければならない。

こちらはCV-ZのEASではなくてスプール側だ
それもマグVじゃなくて深溝スプールね
スプール側から考えてみよう。EASの画像だと誘導電流は奥から手前に流れているが、これをスプール側を基準にすると手前から奥の方向に流れていることになる。で、磁界中の導体に電流が流れると導体には電磁力が発生する。今度はモーターの動作原理と同じだ。この時の電磁力の向きは「フレミングの左手の法則」によって求めることができる。

左手は本来こういった使い方をするためにあるのではない
もちろんリールのハンドルを巻くために存在するに決まっているぞ!
これをCV-Zのスプールに当てはめてみる。中指を奥方向、人差し指は下に向けよう。すると親指がどうなるかといえば左側を向くようになるはずだ。スプール回転の矢印は左から右に向かっているから、左に向かっている電磁力はスプールの回転とは反対方向の力になる。このスプール回転と反対方向の電磁力がマグブレーキの制動力の正体なのであった。ちなみに磁力線の方向がたとえ逆であっても最終的な結果である電磁力の方向は変わらない。というか、CV-Zのマグネットで内側と外側のどちらがN極かS極かは知らない・・・
さぁ、最後は上級編だ。上級編は「遠心ブレーキの制動力は、スプール回転数の2乗に比例する」のと「マグブレーキの制動力は、スプール回転数に比例する」のが本当かどうかを検証してみる。
遠心ブレーキの場合はこうだと思う (思うっていうコメント自体が、すでにいい加減さを物語っている・・・)
質量をm、回転半径をr、回転角速度をωとすると遠心力Wは、
W=m・r・ω^2
こんな式で求めることができる。
mはブレーキブロックの質量、rはリムの半径だからいいだろう。角速度ωというのは単位時間あたりの回転角度のことだ。だから1秒間に1回転すると角速度は360度毎秒と表現することができる。これを2πラジアン毎秒(rad/s)とも表現している。回転数をNとして、回転数と角速度(rad/s)の関係は、一般的に回転数は1分間あたりの回転数rpmで表すので、
ω=(2・π・N)/60
になり、W=の式のωに(2・π・N)/60を代入して計算してやれば
W=0.01・m・r・N^2
という結果になる。一方、制動力自体は摩擦力なのでさらに計算しなければならないが、BG7001HSの改造編で摩擦力については述べた。
F=μ・W
摩擦力Fは摩擦係数μと荷重Wとの1次関数だ。なので、ここにW=の式を代入してやろう。
F=0.01・μ・m・r・N^2
多少間違っていたとしても、だいたいこんな感じかな。重要なのは「遠心ブレーキの制動力は回転数の2乗に比例する」のを求めることなので・・・。なお、この式の変動要因は基本的には回転数Nだけだ。質量mはブレーキブロックが決まれば同じだし、回転半径rは常に一定だ。ただ摩擦係数μについては水分の影響で変動することはもちろんあり得る。それにしても、この遠心ブレーキってものすごくシンプルなシステムなのだが、21世紀の現代でも充分すぎるくらいに通用するのだから、これを開発した人って偉いと思うぞ。
最後はマグブレーキ、まずは誘導起電力から
磁束密度をB、導体の長さをL、運動速度をVとすると誘導起電力eは、
e=B・L・V
磁束密度Bとは磁力の強さでいいだろう。単位はT(テスラ)と呼ぶらしい。ステラの親戚?と思ってしまう。磁界に垂直な、単位面積あたりの磁力線の数というのが正解か?。導体の長さLはインダクトローターの長さ、これは可変式のマグフォースVだと磁界の影響を受けるローターの長さになる。運動速度Vはインダクトローターの周速度だ。ちなみに周速度Vと回転数Nとの関係は、
V=(2・π・r・N)/60
上の角速度ωによく似ているが、角速度に回転半径rをかけたのが周速度になる。
一方の電磁力はというと、磁束密度をB、導体の長さをL、電流をIとするとこんな式だ。
F=B・L・I
誘導起電力eが発生すれば導体の電流の流しやすさ、すなわち抵抗値Rによって電流Iは決まってくる。
I=e/R
ここでオームの法則を持ち出してもいいのかな?抵抗Rはインダクトローターの材質による固有の電気抵抗係数と断面積によって影響されるだろう。これらの式をF=で表すとこうなる。
F=(B^2・L^2・π・r・N)/(30・R)
=0.105・B^2・L^2・r・N/R
回転数Nが分子にあり、そして2乗ではない。なので、電磁力Fは回転数Nに比例することがこれで何とか証明できたと思う。ただ、正直いって電磁誘導は遠心力よりもなおさら自信がない。現役学生諸君やアタマのいい人の審判を仰ぎたいと思っているのだが、いかがだろうか?
ここでひとつ、スーパー胴付改の超TYPE-R+仕様ローターなのだが、アルミの薄肉だから電気抵抗係数と断面積を考慮すれば銅の厚肉ローターと比較すればかなり誘導電流を流しにくいことになるだろう。よって「飛ばせ、鉄拳!フルキャスト編」で制動力が足らなかったというのは今回の考察で証明できたと思う。また、初期ダイワのインダクトローターが銅なのも、「誘導電流をできるだけ大きくする」という意味では正解のように思える。まぁ、これに当てはまらないアルミローターのPT10Zなんていうリールも存在していたのも事実だったりするのだが・・・
さて、理論武装もできたことだし、それじゃあフルキャスト編へいってみよう!ってリールがないやんけ!!(2006/8/19更新)