「そしたら次は、フックの第二法則をやるぞ」

「え〜っと、第二法則って、どんなコトなのかなっ？」

「第一法則は概略説明やったけど、第二法則は実際のフッキングの動作についての力学的考察やな」

「じゃぁ、力学って言ってるくらいだからっ･･･、結構難しくなるんだっ？」

「いや、高卒レベルなら解読できると思う、ちゅーか、ウチの最終学歴って高校やんか、大卒のかしこいヒトみたいな分析はできへんからな」

「そうなんだよね〜っ、Gamくんって、そんな風には見えないんだけどねっ」

「ははは、ウチには学がないけどなぁ･･･、そしたら本題、まずはこれを見てくれるか？」

コレっ、どうしたのっ？
ウチがイラレで作ってん

「コレって･･･」

「見ただけで意味わかる？」

「え〜っ、何かなっ･･･、ちょっと･･･」

「フッキングの概念図やわ」

「あっ、そうなのっ？」

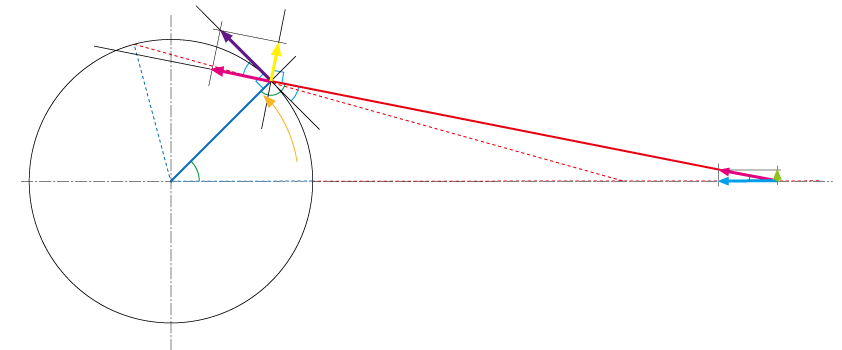
「うん、フッキングってバットエンドが支点、ってのは第一法則で述べてるやんね、この条件で竿を立てる動き、ってのはバットエンドを中心とした回転運動の一部分、って考えてほしいねん」

「じゃぁ、･･･円の半径、青い線が竿で、そこから引っぱってる赤い線が糸、でいいんだねっ」

「正解、実線の青線は45度の場合やけど、点線の赤線と青線もあるやんね？」

「そうだねっ、ちょっと見にくいけど水平の点線と、あと、100度くらいのところにも点線があるねっ」

「うん、図上での角度は適当やけど、90度を超えてるのは間違いないよね、で、この図は竿の曲がりやらガイド、糸フケとか伸びみたいな要因は考慮せずに、できるだけ単純でわかりやすく考えられるようにした」

「そんなのを考えると、すっごく難しくなる、みたいなっ･･･」

「たぶん難しい、ちゅーか、意味不明やもん、まぁ、力学的に理想の状態、って考えてくれたらいいよ、さっき言うた竿の曲がりとかを考慮すると効率は低下することになるし、ウチのアタマでリールとかガイドやら竿の反発力を介在させるのはムリやから、概念としては曲がらん延べ竿になるけど･･･」

「ふ〜んっ」

「そしたらまずはフッキングの動作やねんけど、2つに分けて考えよか？」

「それって？」

「前半後半、って考え方やねんけど、わかる？」

「ちょっと、わかんないけど･･･」

「前半は糸フケの解消で、後半はサカナに対する貫徹力、って考え方やな」

「『かんてつりょく』っ？･･･」

「前半は簡単やんね、フッキング前にリールを巻いても取りきれん糸フケは竿を振って解消する、ってことやんか」

「うんっ、それはわかるよっ」

「で、後半やけど、貫徹力って普段のウチの言い方では『アゴをブチ抜く』って表現になるけど、サカナにフッキングの力、貫徹力が作用するのは糸フケが解消されてからやからこの時点で竿に対する負荷が変わるねんな、だから今回はこういう分け方で考えてみよう、そしたら、この図から見てくれる？

図を作るのって意外と大変なんだねっ
おおきに、わかってくれた？

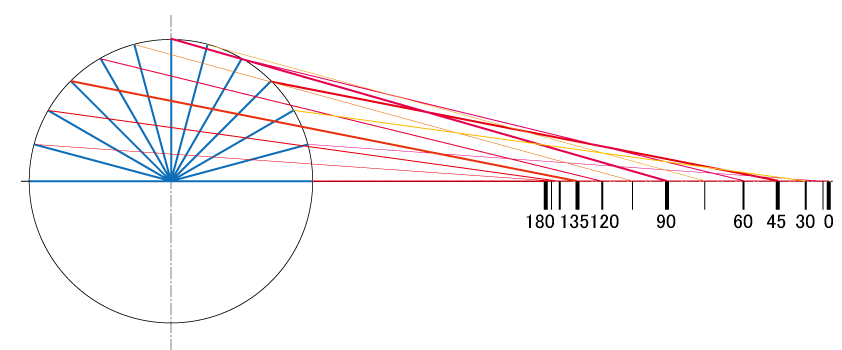
これは15度刻みで0度から180度の回転運動を水平方向の移動量に変換した図やけど、一目瞭然で15度とか30度みたいな浅い角度よりも75度とか90度みたいに立ってる角度の方が同じ角度を動かしても移動量そのものは大きいよね？」

「竿の角度で移動量って違うんだっ･･･、同じだけ動かしてるからどこでも同じなのかな、って思ったんだけど、違うのっ？」

「竿は回転運動やけど糸の動きは回転運動じゃないからな、これがリールに巻く場合なんかを想像したらいいけど、糸も回転運動になるんやったら角度は関係無しで同じ分だけ動くねんけど、直線運動になるとその移動量はこの図みたいに角度に依存すると思う」

「ふ〜んっ･･･」

「だから、フッキングで0度から動かした場合は最初の15度近辺は移動量にはあんまり貢献していない、ってのがこの図でわかると思う」

「うんっ、最初は全然動いてないんだねっ」

「フルフッキングしてるつもりでも水平もしくは浅い角度からのフルフッキングは効率が悪い、ってのがこの図から導き出せるし、水平以下の角度から始めるのは論外やと思う、移動量、要するに糸フケの解消には貢献してない」

「･･･」

「今のウチの考えやけど、30度からフッキングを開始して、その分竿を後ろ、鈍角に振れば･･･、例えば120度くらいまで振ってあげればもっと効率のいいフッキングになる、少なくとも水平から開始して90度までのフッキングに比べると動かす角度は同じ90度やけど効率は良くなると思うわ」

「Gamくん、この図を見たら浅い角度じゃなくって、もっと竿が立った状態からフッキングすればいい、ってコトはわかるし、第一法則でも竿をおっきく動かす、ってコトだったよねっ、だからねっ、それは理解できるんだけど、実際に120度とかそんな角度って、難しくないっ？、フツーに考えると体が邪魔でそんなに後ろまで動かせないと思うんだけど･･･」

「うーん･･･、例えば体を正面に向けるんじゃなくって斜めに向ける、竿も真上に立てるんじゃなくって斜めに体から逃がすように振れば120度近辺なら動かせるわ、ただ、体が逃げてるからどうしても力は入りにくくなるけど･･･」

「やっぱ、難しいんだねっ･･･、ところで、Gamくんはフッキングってどうしてるのっ？、さっき言ってたみたいに竿を斜めに振ってるのかなっ？」

「いや、ウチは斜めどころか真横に振ってるよ」

「真横っ？わかんないよっ･･･」

「リアグリップを脇差ししてしっかり保持してから体全体で回ってフッキングしてるわ、これやとヤル気になったら180度、真後ろまで竿が振れるし、体全体で保持しながら竿を動かすから力の入り具合も問題ないと思う」

「へ〜っ、そういう方法があるんだっ」

「ああ、大阪時代から『雷撃フッキング』とか言うてやってたけど、万人にはお勧めできんなぁ･･･」

「それはどうしてっ？」

「まず、体が正面じゃなくってあさっての方向に向いてるやん、それとファイト中はバットエンドをお腹に当てるけど、バットエンドを脇差し状態からお腹に戻す必要があるからワンテンポ遅れるんやね」

「初めの対応が遅れちゃうんだねっ」

「それに、後ろに振りすぎたら竿が折れるぞ、糸と竿の角度が鋭角になるからな、ウチもさすがに180度とか極端な角度には振ってないもん」

「Gamくんって、どれくらいまで竿を振ってるのっ？」

「どうかなぁ･･･、感覚的な話しになるからなんとも言えんけど、気持ちだけは180度回すつもりでフルフッキングしてる、ただ、現実的にはそんなに振れてないわ、120度とかそんなんと違うかな？」

「じゃぁ･･･、Gamくんって、竿、折ったコトってあったっけ？」

「『バンブーカムルチィ』は『雷撃フッキング』でへし折ったなぁ･･･」

「でもっ、あれって、･･･フェルールの部分の問題じゃなかったのっ？」

「そうとも言うけど、ちゅーか･･･」

「･･･あ〜っ、わかった〜っ！、また、放置してるんだねっ」

「ブランクは仕入れた、･･･って最近こればっかりやなぁ、一応、バンブーのソルトブランクは入手済みやけど、そこまで手が回らんよ」

「ぷぷぷっ♪」

「･･･そしたら話し戻すけど、結局、フッキングで移動距離を稼ぎたい場合は折れんような竿を使うことになるよなぁ、少なくとも高弾性カーボンの竿で鈍角に振るのはやめた方がいいと思うわ」

「折れない竿？、そんなのって、あるんだっ？」

「硬い竿を使え、ってのが一つと、硬いのが嫌いな人は、高弾性カーボンじゃなくってグラスコンポジットとかあの辺かな？」

「やっぱ、Gamくん的には、硬い竿の方がいい、みたいなっ」

「うん、『竿の硬いは七難隠す』って感じやわ」

「それっ、何かのことわざかなっ？」

「正解は『色の白いは七難隠す』･･･」

「どういう意味だっけ？」

「いや、ミキは気にするな、次行こう･･･、次は後半の貫徹力についてやけど、一番上の図の青線と赤線の交点部分を見てほしい･･･

ここが一番難しそうだねっ
そうやなぁ･･･

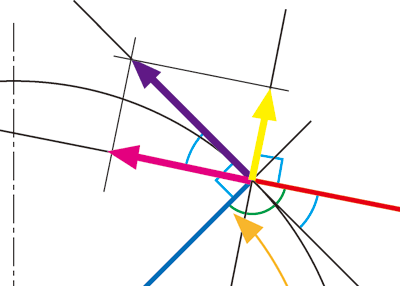
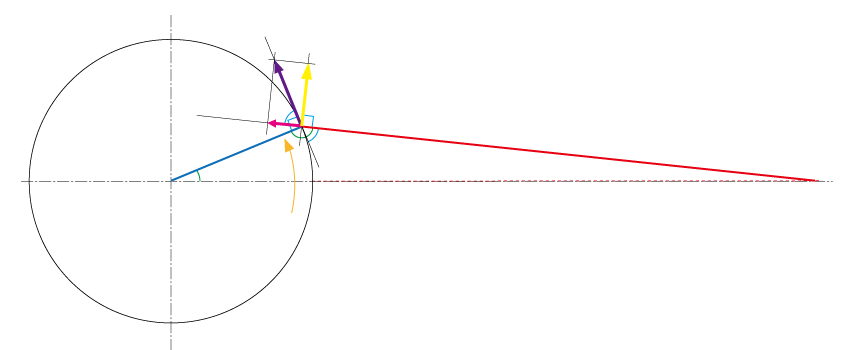
この図で青い線と直角に紫の矢印があるやんね？」

「うんっ」

「これは第一法則でコメントした『てこの原理』によりティップに発生した力、って考えてほしい、回転運動として考えると、円の接線方向に発生する力が紫の矢印やねんな」

「･･･」

「で、この図は糸と竿が直角じゃないよね？」

「その場合って、紫の力がそのままが糸に伝わるんじゃなくって･･･、この図だと分力してる、みたいなっ･･･」

「そうそう、さすがウチより現役が近いだけのことはある、ミキの言うとおり紫の力を分力したのがピンクと黄色の矢印やんね」

「うんっ、糸に平行なのがピンクの矢印で、垂直なのが黄色の矢印だよねっ」

「フッキングに必要なのは赤線に平行なピンクやねんけど、･･･まず、ここで分力されてる、ってことはパワーロスが生じてる、ってことになるよね？」

「そうだねっ、紫よりもピンクの矢印の方が短いもんねっ、･･･じゃぁ、紫とピンクが同じ長さになるようにすればパワーロスは生じない、ってコトになるんだっ」

「理屈はそうなる、赤線と青線が直角の場合は紫イコールピンクやねんから、竿と糸が直角なる角度が力の伝達としては理想の領域やわ、こんな感じで･･･」

図は簡単だけど･･･
実戦的には？やわ

「でもっ、コレってすっごく難しそう･･･、竿の長さはかわんないけど、糸の長さって結構かわっちゃうよねっ」

「だからあくまで屁理屈の世界な、この竿と糸が直角になる角度はそれぞれの長さがあれば計算できるけど、竿って曲がるから計算される角度よりもさらに大きく動かす必要があるわ」

「･･･」

「そしたら次は竿が浅い角度の場合を見てもらおう･･･

Gamくん、右の矢印、書いてないよっ、忘れたんじゃないのっ
気にするな、力が小さい場合は無視できるねんって･･･

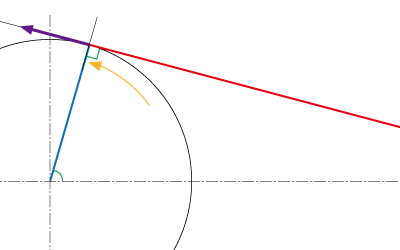
今度は上の図の半分、22.5度の場合やねんけど、円の接線方向の力、紫の矢印は同じ大きさやけど、ピンクの矢印はさっきとは全然違うよね」

「うんっ、かなり違うんだね〜っ」

「角度が浅い場合はこんな感じでフッキングに必要な糸を引っ張る力は少なくなる、･･･ただ、実戦的にはこの浅い角度で糸フケが解消された場合はトータルでの貫徹力はもちろん大きくなるよね」

「そうだねっ、実際には竿を立てちゃうワケだからっ、･･･力を加えられる範囲が広くなるもんねっ」

「うん、そんな感じや、ほんなら次やけど･･･

水色の矢印って、ちょっと、ゆがんでないっ？
うっ･･･

今まではティップ側での話しで、そのティップで発生した力が何に作用するか･･･」

「結局、フッキングってサカナに作用するんだからっ、この図はフックの部分だから、コレが貫徹力になるんだねっ」

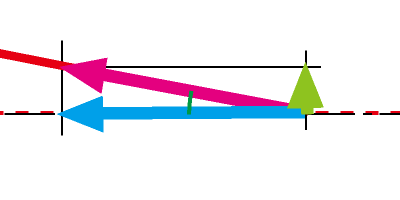
「そう、･･･糸に平行なピンクの矢印がそのまま伝わったと仮定する、で、この図では位置としては支点の延長線上になってるよね？」

「うんっ、でも･･･、これもわかりやすくしたからでしょっ、実際の位置はもっと下になるもんねっ」

「バットエンドとフックが同一平面上ってのは実際にはあり得んやんか、フック位置を下にずらした場合を想定するのがホンマやけど、面倒やから今回はこれでいい、それでな、見ての通りで、引っ張る方向は糸になるけど、実際に作用する方向は水平面、これはサカナの姿勢に依存するけど今回も無視しよう･･･、で、この場合って糸は水平面に対して角度がついてる、そうなると･･･」

「ここでも図の通り、水平の水色の矢印と垂直方向の緑の矢印に分力されるんだねっ」

「理屈的にはそう、実際に作用するのが水色の力やねんけど、現実的には距離が遠い場合、竿の長さに対して糸が充分に長い場合はここの角度は小さくなるよね？」

「･･･え〜っと、そんな感じかなっ」

「ここの角度が小さい場合はピンクと水色ってほぼイコール、分力は無視してもいい、逆に言うと近距離の場合はここの角度が大きくなるのでピンクに対して水色は分力されて小さくなるのと、フックで貫通させるのには余計な方向の垂直の力、緑の矢印が無視できなくなる」

「Gamくん、そのっ、余計な力、ってコトだけど･･･」

「フッキングってフックが引っ張られてサカナのアゴにフックを突き刺すやんね、それは水平方向の力によって成り立つねんけど、垂直方向の力ってサカナのアゴを上に開ける方向に作用するやん」

「･･･」

「アゴを開ける、ってことは貫通しにくい、ヘタをするとスッポ抜けすることも考えられるわ」

「じゃぁ、スッポ抜けって、ここの力が要因ってコトなんだっ」

「いや、それだけじゃないと思う、ただ、近距離でスッポ抜けが発生する場合はこれを要因の一つとして考慮する必要があると思う」

「遠い場合は関係なさそうっ？」

「うん、さっきも言うたけど、遠距離の場合はこの緑の力は無視できるはず、ただ、サカナの姿勢等の条件によっては上向きの力が有効に作用するケース、ってのも考えられんでもない」

「えっ、それって？」

「フックって貫通するだけじゃなくって、初動としては、まず、口腔内にフックポイントを突き立てる、それから貫通云々の話しになると思う」

「･･･」

「そうなると、条件次第ではフックポイントを突き立てる、ってのに上向きの力が作用するかも？ってことやねんけど･･･」

「じゃぁ、疑問符なんだっ？」

「うん、その辺は第三法則で詳しく見ていくことにしよ、･･･それ以外やと投げ降ろし、ってロケーションになると角度がつくからちょっとは考えんといかん気がする」

「投げ降ろし、って？」

「水面よりも3メートルとか結構高い場所から投げる場合やな、ポイントによってはどうしても投げ降ろしになるケースもあるけど、フッキングだけを考えればできるだけ糸と水面の角度は小さい方がいい、ってのは理解できるよね？」

「うんっ、糸を引っ張る力がそのままフックを引っ張る力になるのと、アゴを開く力が発生しないんだねっ」

「次行こう･･･、まぁ、今まで図上で色々コメントつけてるけど、今度は実際にどんな結果になるのかを計算してみよう、移動量で必要なのは竿と糸の長さ、それに竿の角度があればいいし、力を求める場合はフロントグリップに加える力とバットエンドからグリップまでの長さが必要なパラメータになるわ」

「あっ、計算でもきちゃうんだっ？」

「基本は三角形やねんから三角関数の応用やん」

「三角関数って、サイン、コサイン、タンジェント、それだけで大丈夫なんだねっ、･･･でもっ、どうやって計算するんだっけ？」

「そこまでは覚えてない？」

「･･･だって、三角関数なんて普段使わないじゃん、そんなのって、日常生活じゃぁ全然必要ないんだもんっ」

「ミキって、そういう言い訳して勉強サボってたクチやな」

「･･･」

「ビンゴか？」

「もう、いいよっ･･･」

「ははは、実は、ウチもミキのこと言えんのやな、『大日本帝国万歳！』とか言うて英語サボってたから、やっぱしそういうツケって、いつか回ってくるねん」

「そうそう、Gamくんって、英語は全然ダメなんだよねっ」

「嬉しそうに言うてるわ･･･」

「それはGamくんの被害妄想だよ〜っ、そうじゃなくって、誰にでも苦手ってあるんだよね、ってお話しだよっ」

「あぁ、そんな感じやな･･･、そしたらこれで･･･

とやかく言う気はないけど、基本中の基本やから、おさらいするで、･･･この直角三角形の角度αについて考えるねんけど、垂線がＡで、底辺がＢ、斜辺がＣやんね、このときの三角関数はこんなんになるわ」

「･･･何か、そう言われると、こんなのだったかな〜、って気がする･･･」

「わかってくれた？」

「なんとなく、だけど･･･」

「そしたら本題、『変態フッキング三角関数』やな･･･

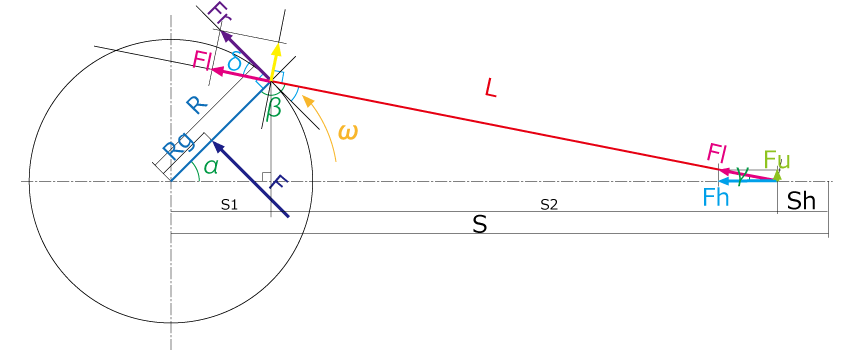
コレっ、いつもの「変態」なんだっ･･･
うん、「変態コンセプト」に基づいた力学的考察やもん

これ、難しそうか？」

「･･･」

「この『変態フッキング三角関数』で必要なパラメータはさっきも言うたけど、

• 竿の長さ・・・Ｒ
• 糸の長さ・・・Ｌ
• 竿の振り角度・・・α
• バットエンド〜フロントグリップ長・・・Ｒｇ
• グリップに加える力・・・Ｆ

これだけで他の値も全部計算できるよ」

「そう言われると、なんか、簡単そうに思えるんだけど･･･、でもっ･･･」

「ぱっと見でややこしそうに思えるからなぁ･･･、ホンマはミキに全部計算してほしいねんけど、今回はやめとこ」

「そうなんだっ」

「ちょっと、ほっとしたか？」

「･･･」

「ははは、まぁ、見てる人も興味があるのは結果だけやと思う、だからこの図が正解なんかを検証するような物好きはおらんと思うからウチが計算するわ、実際の式としてはこんなんになるよ」

「へ〜っ･･･、いろんな式があるみたいだけど、全部さっき言ってた数値から計算できるんだねっ」

「うん、そんなにややこしくないと思うけどなぁ、基本中の基本、中学生レベルと違うか？」

「･･･あれっ？ねぇ、Gamくん、この式には竿と糸の角度が直角になる場合の竿の角度ってないんだけど、あれも計算できる、って言ってたよねっ？」

「あっ、ごめん、忘れてたわ･･･、そしたらミキが式を考えてくれ、それくらいやったらわかるのと違う？」

「え〜っと･･･」

「難しい？」

「ちょっと待っててっ、･･･竿と糸が直角っ、コレって竿が底辺で糸が垂線になるんだからっ･･･、そうそう、タンジェントの式でいいんだよねっ！」

「で、具体的には？」

「タンジェントあるふぁ〜いこ〜るっ、糸の長さ割る竿の長さ、だねっ」

「それを逆三角関数、アークタンジェントでαの式にするねんけど、『ミキちゃん語』をそのまま文章にするとめっちゃわかりにくい、通訳するわ･･･

こんな式になるねんで」

「って言うか、それっ、Gamくんが忘れてたんだよっ」

「いや、まぁ･･･、とにかくこの式に、竿の長さやら糸の長さ、角度や力を色々なケースを想定、実戦的な数字を代入するんやね」

「じゃぁ、長い竿とか短い竿、この辺りみたいな足元や遠くに投げちゃう場合、ってコトだねっ」

「うん、そんな感じやわ、そしたら関数電卓で計算してみるけど･･･

条件その1・・・Ｒ＝2.286m(7ft6inch)、Ｌ＝30m、Ｒｇ＝0.57m、Ｆ＝10kg、αは15度刻みで0〜180度

えーっと･･･、この条件その1は竿が『GUN2ZERO』の『アルガマスター』やねん、ウチがビルドした竿みたいな特殊条件じゃなくって、ごく一般的な状況、ってのを想定した」

「Gamくんの持ってる竿でこれだけが市販のライギョ竿なんだったよねっ、でねっ、グリップの長さって実際に測った長さなんだねっ」

「そうやな、フロントグリップ中心からバットエンドまでの長さになる、ちなみに竿の長さは実測じゃなくって公称長さのフィートをメートルに換算した値を採用した」

「それって何かワケがある、とかっ？」

「測るのんめんどくさい･･･」

「あ〜っ、手を抜いちゃってる〜っ！」

「そんなんどーでもええねんって、単位がメートルやねんから1センチとか2センチなんか誤差の範囲やぞ、それよりも公称長さの方がわかりやすいと思うけどなぁ、市販竿やし･･･」

「そんなのでいいのっ？せっかく色々計算してるんだからっ、ちゃんとした長さで計算した方がいいと思うんだけど･･･」

「ウチがええって言うてるからそれでいい･･･、で、糸の長さもウチがフツーのヒシ池なんかで想定してる捕食距離、なんぼ大遠投とか言うても現実的にはだいたいこの近辺って思う、そしたら計算結果の表やけど、重要なんはいつもみたいに黄色にしてる、だからβとかγはあまり気にしなくていいわ」

「じゃぁ、この赤って？」

「赤は比較のために色を付けた」

「あとねっ、表が2つあるじゃないっ、上はさっき言ってた値ってわかるけど、下の表って？」

「上の表にあるＳhって数字は0度を基準とした移動距離やけど、下は15度刻みでの移動量やねん、だからこの数値が大きくなると同じ15度の振り幅でも効率がいい、って考えてくれたらいいよ」

「それじゃぁ、この表で大事なのはフックを引っ張る力Ｆhと15度刻みの移動量･･･」

「それとティップに発生する力Ｆrとβが90度になる場合の竿の振り角度α90やんね、まずはＦhやけど、この条件ではＦhとＦlって変わらへんやんか？」

「それっ、先に言ってたねっ、･･･距離が遠い場合はかわんない、って」

「γが4度くらいの場合はこうなるわ、次はティップに発生する力Ｆr、グリップで10キロ加えたと仮定しても1/4くらいになってるやん」

「うんっ、意外と少なくなるんだねっ」

「だからフロントグリップ位置って力を考えると結構重要なのかも知れんわ･･･」

「Gamくんってロッドビルドするでしょっ、そのっ、グリップの位置って考えてるっ？」

「いや、一部の例外を除けば適当やな、ただ、理屈では長ければいい、ってことになるけど、現実的には手が届く範囲ってあるやんか」

「あんまり長くすると手が届かなくなるよねっ」

「多少長くした程度では誤差の範囲、ってことになるし、個人の体格にも依存するやんね」

「身長とか腕の長さ、だよねっ」

「自分で竿を組む場合はそれも考慮できるから、今度からは考慮に入れるよ」

「それじゃぁ、次はα90だけど、この条件だと90度近くになるんだねっ」

「そうやな、距離が遠ければ遠いほどαは90度に近づくわ、逆に距離が近ければそんなに竿を振り回さんでもいい、これはもちろん近距離やとパワーロスが少ない、ってのも含んでるわ」

「距離が近いと糸フケも少ないし、効率が良くなるもんねっ」

「そしたら最後の移動量になるけど、15度刻みでの最大移動量は75度から90度の範囲で、60センチになるやん」

「そうだねっ」

「ほんならさっき言うたけど、0度から90度で竿を振る場合と、30度から120度まで振る場合を比較してくれる？」

「0度から90度までの場合はＳhがそのままだから2.37メートルだよねっ、30度から120度の場合って、120度のＳhから30度のＳhを引けばいいから･･･、3.16メートルになるよっ」

「3.16マイナス2.37は0.79で約80センチやん、この80センチって差をどう考えるか、ってことやけど･･･、ウチ的には条件が悪くなればなるほどこの差は有効に作用すると思う」

「じゃぁ、カバーとか、第一法則で言ったのを考えた場合は、ってコトなんだねっ」

「うん、ライギョ釣りって糸フケが結構出る釣りやと思う、80センチなんかたかが高速ベイトリールのハンドル1回転分、と言えばそれまでやけど」

「でもっ、それって、一番いい場合の巻き取り量だったよねっ、糸が出てる場合はもっと少なくなる、って･･･」

「もちろんフッキングする前に余分な糸フケは巻き取るねんけど、いつもそれが確実にできるか、って言えば違うと思う、悪条件下では竿を大きく振ることによる糸フケの解消、ってのを積極的に狙っていい、いや、狙うべきやと思うわ」

「あのねっ、･･･30度からじゃなくって、0度から120度まで振ってあげればもっといいんじゃないっ？、計算すると3.49メートルになるもんねっ」

「･･･今の話しって同じ角度での比較、って前提やんか、せやから実戦的には30度以下の領域を有効活用してあげたらもっといいと思うよ、ただ、その効果は90度以降の角度を活用することに比べると少ないから、どうせ動かすなら前じゃなくって後ろを意識した方がいい、少なくとも必ず水平に寝かせてからフッキングする必要はない、ってのがウチの考えやわ」

「でもっ、程々にしないと竿が折れちゃうかも･･･」

「そうやなぁ、最後はタックルバランスの話しになるのかな？、･･･そしたら色々な条件当てはめて計算しよか」

「うんっ」

条件その2・・・Ｒ＝2.286m(7ft6inch)、Ｌ＝5m、Ｒｇ＝0.57m、Ｆ＝10kg、αは15度刻みで0〜180度

「条件その2は糸の長さだけ変えてみた、5メートルやな」

「じゃぁ、足元なんだねっ」

「うん、この近辺のクリーク打ちを想定してみた」

「この表を見ると･･･、そうだねっ、上向きの力Ｆuがおっきくなってるんだねっ」

「あとはα90が結構変わってるやんか」

「え〜っと、条件その1は85度で条件その2は65度だから、20度くらい違うねっ」

「一応、こんな感じで力の伝達については効率のいい角度も小さくなるからそんなに後ろに竿を振る必要性がない、ってことかな？」

「でもっ、実際には距離が近いから力の伝達や糸フケって、あんまり考えなくってもいいんだよねっ」

「ただ、上向きの力はミキの言うとおり結構変大きくなってる」

「条件その1だと無視してもいい、ってコトだったけど、今回はフックを引っ張る力の半分くらいになっちゃうからそうも行かない、みたいなっ･･･」

「うーん･･･、この力を少なくすることを考えると、やっぱり竿を立てて合わせるんじゃなくって、水平やら場所が許せば下向きとか、要は糸と水平面との角度をできるだけ小さくする、って感じと違うか？」

「･･･今回はバットエンドとフックが水平、って考えでしょっ、でもっ、実際にはそうじゃなくってフックが水平よりも下になるからもっと角度がおっきくなるよねっ、だからっ、距離が短いほど上向きの力って影響がおっきくなる、でいいのかなっ？」

「理屈はそうなる、ただ、やっぱりサカナの姿勢とかフック形状やらいろんな条件を考慮する必要があるわ」

「さっきも言ってたけど、疑問符なんだねっ」

「そう言うこと、そしたら次やけど、表と解説ばっかりが続くと面白くなくなるから全部まとめるわ･･･

• 条件その1・・・アルガマスター 通常距離、Ｒ＝2.286m(7ft6inch)、Ｌ＝30m、Ｒｇ＝0.57m、Ｆ＝10kg
• 条件その2・・・アルガマスター 至近距離、Ｒ＝2.286m(7ft6inch)、Ｌ＝5m、Ｒｇ＝0.57m、Ｆ＝10kg
• 条件その3・・・カマジャ83ポッピング 通常距離、Ｒ＝2.515m(8ft3inch)、Ｌ＝30m、Ｒｇ＝0.66m、Ｆ＝10kg
• 条件その4・・・南山・蛇頭殺 通常距離、Ｒ＝1.520m(5ft)、Ｌ＝30m、Ｒｇ＝0.42m、Ｆ＝10kg
• 条件その5・・・南山・蛇頭殺 至近距離、Ｒ＝1.520m(5ft)、Ｌ＝5m、Ｒｇ＝0.42m、Ｆ＝10kg
• 条件その6・・・秋水・蛇頭殺 通常距離、Ｒ＝1.805m(6ft3inch-0.1m)、Ｌ＝30m、Ｒｇ＝0.55m（0.65m-0.1m)、Ｆ＝10kg
• 条件その7・・・アルガマスター 通常距離、Ｒ＝2.186m(7ft6inch-0.1m)、Ｌ＝30m、Ｒｇ＝0.47m(0.57m-0.1m)、Ｆ＝10kg

条件その1とその2はさっき説明したから省くで、･･･条件その3はロングロッドやねんけど、ウチが持ってる竿で8フィートを超えるのはソルトロッドしかないからGTロッドでやってみた」

「条件その4とその5は短い竿、Gamくんが作った竿での計算だねっ、･･･それでねっ、条件その6とその7って、竿とグリップの長さが引き算して短くなってるけど、コレってっ？」

「その6とその7は脇差しでフッキングした場合を想定して長さを10センチ短くした、ウチが脇差し用にビルドした竿と市販竿の比較、って考えてくれたらいい」

「そのっ、脇差し用、ってコトなんだけど、どう違うのかなっ？」

「フロントグリップ位置がフツーの竿に比べて前よりになってるわ、ただ、3年前に組んだ竿やから今回みたいな力の大きさに対する配慮じゃなくって、単純に脇差しで手が届く範囲、ってことやねん、詳しくはこっち見てくれたらいと思う、3年前と今では考えが変わってきてるから自分でも恥ずかしいけどな」

「ふ〜んっ･･･、でもっ、この時も『てこの原理』ってコメントしてるじゃんっ、やっぱ、3年前から考えてたんだっ、それに、さっき言ってた一部の例外、ってこの竿のコトなんだねっ」

「うん、ウチがビルドした竿でフロントグリップ位置を考慮したのは『秋水・蛇頭殺』だけやわ、でもな、ちゃんと読んでくれたらわかるけどあの当時は『てこの原理』についてはこじつけみたいなとこがあったぞ、今、ビルドするんやったらやったら堂々とコメントするけどな、そしたら計算結果、発表するわ･･･

どうやろか、これって？」

「どうやろか、って言われても･･･、最初の3つが前半の移動量で、それ以降が後半だよねっ、だから･･･、やっぱ、長い竿の方が移動量はおっきいし、短い竿で移動量をおっきくしようとするともっと後ろに動かす必要がある、みたいなっ･･･」

「そうやな、結果的には竿の長さに比例してるわ」

「あとっ、糸の長さが短い方が移動量はおっきくなってる、0度から90度の場合って竿が長い条件その3よりもその2の方がおっきいよねっ」

「180度振った場合の最終的な移動量は竿の長さの2倍にしかならない、でも、回転運動を直線運動に変換した場合って途中の結果が変わるみたいやな、･･･まぁ、至近距離での移動量って実戦的には考慮する必要はないけど」

「それ以外だと･･･、力については、Gamくんの作った竿、条件その7が一番おっきいねっ、やっぱ、それ用に作ったからかなっ？」

「力の場合はフロントグリップ長に比例して、竿の長さに反比例してる、だからフロントグリップ位置を考慮することによって長い竿でも発生する力は大きくできるわ、条件その3のGTロッドみたいに」

「実際には手の届く範囲、だよねっ」

「まぁ、そんなとこやな、あとはやな･･･、至近距離の場合はやっぱり上向きの力が大きい、今、思い浮かぶ対策は竿と水面との角度をできるだけ小さくするようなフッキングを心がけるくらいやな･･･」

「だいたいこんな感じかなっ？」

「うーん･･･、あとはフツーのフッキングと『脇差し雷撃フッキング』の比較、その1とその7の比較になるけど、移動量は若干短いくらいで済んでるよね？」

「長さを10センチ引いただけだから、だねっ」

「この程度ならそんなに問題にならんと思う、でも、力の差は結構あるよね？」

「計算すると、･･･86パーセントだよっ、結構な差になるから、脇差しにするとおっきな力でフッキングする必要があるんだねっ」

「こう見るとたいしたことない、って感じると思う･･･、まぁ、その代わり後ろに振り回すことができるからトータルの貫徹力は増えるのと違うかな？」

「もうちょっと、計算が必要かなっ？」

「うーん･･･、そしたら第二法則の最後、より実戦形式に近いカタチでやってみるか」

「それって？」

「フッキングの前半後半で竿を振る役割が違う、ってのはコメントしてるよね」

「前半が糸フケの解消でっ、後半は貫徹力、だよねっ」

「うん、さっきの計算は前半後半関係無しで竿の角度に対する移動量や力を求めたけど、一定量の糸フケを解消したあとの貫徹力、ってことでやってみるわ･･･

至近距離は省いたぞ
距離が近いとあんまり考えなくってもいい、ってコトだねっ

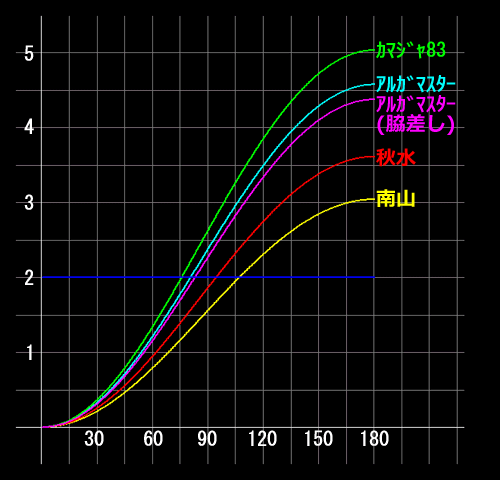
これは移動量を縦軸、竿の角度を横軸でグラフにしたねんけど、こうすれば一定量の糸フケを解消するのに必要な竿の振り角度が一目でわかるよね？」

「うんっ、これならわかりやすいよっ」

「フッキングの開始角度は計算がめんどくさいから0度から始めよ、それで、青線は糸フケを解消するのに必要な移動量、今回はかなり条件悪いけど2メートルと仮定した、で、その青線に達するまでの角度が前半、って考えてくれる？」

「そうだねっ･･･、『カマジャ83』は75度くらいだけど、『南山』は105度くらいまで動かす必要があるよねっ」

「そしたら次、最終的な結果になるねんけど･･･

色はさっきと同じだよねっ
曲線に直接指示できへんからな･･･

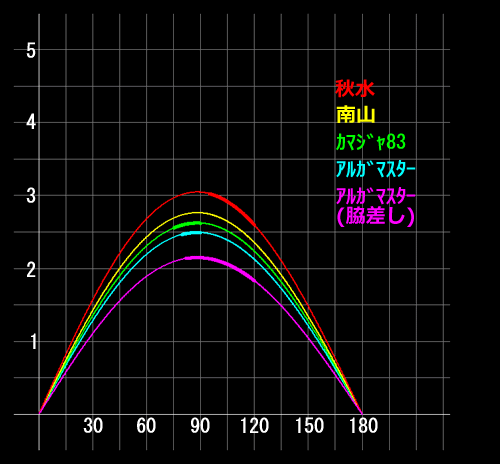
今度は後半やから力が縦軸で角度が横軸になってるわ、ここで見てもらいたいのはグラフの曲線で一部分だけ太い線があるやんね」

「うんっ、コレがさっき言ってた糸フケを解消したあとの貫徹力、ってコトだねっ」

「そう、フツーのフッキングは90度まで、脇差しについては120度まで、って条件つけてみたけど、『アルガマスター』で比較するとフツーのフッキングは確かに力そのものは大きいけど、力を加えることができる範囲が狭いやん」

「この条件だと、だいたい10度くらいになっちゃうんだねっ」

「それに比べると脇差しの場合は力は小さくても加える範囲が広い、40度近くになるからトータルとしての貫徹力は確保できる、これに竿の曲がりを加味するともっと条件が悪くなる･･･、いや、2メートルなんて悪条件はヘビカバエリアになるから曲がりは考慮せんでもいいかも知れんなぁ、竿硬いもん･･･」

「やっぱ、竿の曲がりって計算できないっ？」

「今後の課題にしとくわ･･･、とにかく、竿をなんとかして鈍角に振ってあげることによって最終的な貫徹力を増やすことができるんやね」

「あのねっ、『南山』って太い線がないでしょっ？、この条件だとどうにもならない、みたいなっ･･･」

「うん、極端に短い竿やからな、脇差しすればなんとかなるけど、やっぱり海部郡クリーク打ちの竿やもん、悪条件下で使うもんじゃないよ」

「あとっ、脇差しした『アルガマスター』と『秋水』だけど、貫徹力ってどっちの竿がおっきくなるのかなっ？、なんか、微妙な感じだよねっ」

「そうやなぁ･･･、あのな、太線の角度範囲を指定して積分すればこの曲線と直線で囲われた部分の面積が算出できるやん、それって覚えてる？」

「え〜っと、そんなコト、習ったような気がする･･･、でもっ、積分しないとダメなんだっ･･･」

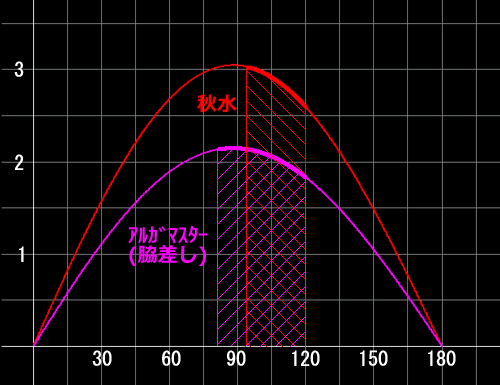
「まぁ、概念としてはこうなる、他に比較のしようがないからな･･･

他の竿はいらないのっ？
目障りやから消そ

ミキ、そしたら積分してくれる？」

「えっ、ミキが計算するのっ･･･」

「って言いたいとこやけどやめとく」

「じゃぁ、どうするのっ？、って言うか、ミキ、三角関数の積分なんてできないけど･･･」

「そう言うのが見え見えやからな、せやからこんなん適当、見た目で比較してみてくれ」

「え〜っ、どうかなっ･･･」

「･･･」

「このピンクと赤の斜線が重なってない部分、コレのどっちがおっきいか、ってコトだよねっ」

「そうやな」

「たぶん、だけど、『アルガマスター』の方がおっきくないっ？」

「正解、これを積分すると『アルガマスター』が約1.35で『秋水』がおよそ1.22になるわ」

「あ〜っ、Gamくん、ちゃんと計算できるのに、ワザと言ってたんだ〜っ！」

「ははは、これはウチが計算したんじゃないんやな、ウチが使ってるグラフ書くソフトって積分もできるねん、結構便利やねんぞ」

「な〜んだっ、そうだったんだっ、･･･でもっ、その数字ってちっちゃいよねっ、2キロとか3キロはあるはずなのに、1.22とか1.35だもんっ」

「三角関数の積分は角度単位が違うわ、『ラジアン』って覚えてる？」

「･･･」

「まぁ、『弧度法』って言い方するけど、フツーの角度単位、『ディグリー』で360度の場合、『ラジアン』では2πになるんやな」

「じゃぁ、例えば30度とかって･･･」

「･･･30割る360掛ける2πは？」

「え〜っと、･･･0.523になるねっ」

「うん、わかりやすい表現ではπ/6やな、だからこんな小さい数字やから面積も小さくなる、ってことでこれが直接の力の大きさを表してるワケじゃない、だから比率で比較した方がいいと思う」

「それだと、･･･『アルガマスター』の方が1割り増しくらいだよっ」

「まぁ、その程度やったら竿の長さを考えると健闘してるのと違うかな？、･･･フッキングは長い竿の方が有利、ってことで第一法則でも述べてるけど、短い竿でもグリップ位置によってはそんなに不利にはならない、って計算結果やんね？」

「『アルガマスター』が7フィート6インチで『秋水』が6フィート3インチでしょっ、長さ、結構違うもんねっ」

「そうやねん、貫徹力を考慮するとフロントグリップ位置って意外と重要なんがこれで理解できると思う」

「うんっ、そうなんだねっ」

「そしたら第二法則はこれで終わりにするけど、まとめ、やってくれる？」

「Gamくん、今回って、色々検討したから難しいよっ･･･」

「うーん･･･、途中、グッチャグチャになってるもんなぁ･･･」

「今回はGamくんがまとめた方がいいと思うよっ」

「そうやなぁ、そしたら･･･

ゴチャゴチャ言わんと硬い竿で後ろを意識して振り回せ！

ミキ、これでええやろ？これが『フルフッキングの正しい姿』、柔らかい竿で後ろに振り回しすぎると折れるからな」

「なんか、すっごく単純･･･」

「ええねんって、能書きなんかアホ臭ぁてやってられへんわ」

「だけど、せっかく色々検討したんだよっ、もうちょっと、･･･結果、反映した方がいいと思うよっ」

「うーん、ほんなら･･･

フッキングにはフロントグリップ位置が意外と関係してくるぞ！

竿の曲がりを考慮せーへん場合、後ろに振り回すのとグリップ位置やね、力学的にはこれ以上コメントのしようがないもん」

「じゃぁ、次は竿の曲がりも計算できるようになったらいいのにねっ」

「･･･それ、もしかして、ウチに対する宿題か？」

「うんっ、そうだよっ、さっきも『今後の課題』って言ってたじゃんっ♪」

「･･･ミキ、そしたら『ヤング率』と『断面二次モーメント』って調べといてくれる？、これ、ウチからの宿題やぞ」

「ちょ、ちょっと〜っ、どうしてそうなるのよ〜っ！」

「いや、ミキからの宿題って竿の曲がりやろ？」

「そうだけど･･･」

「そしたらこれでええやんけ」

「じゃぁ、もしかしてGamくんって、ホントは･･･」

「さぁ、なんのことかな？、そしたら次回、『フックの第三法則？！』はミキの宿題の答えをお楽しみに！」

「もうっ、意味わかんないよっ･･･」

(2009/4/29更新)

一応、もとにもどるけどっ、本当は閉じてねっ